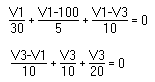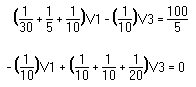In this method, we set up and solve a system of equations in which the unknowns are the voltages at the principal nodes of the circuit. From these nodal voltages the currents in the various branches of the circuit are easily determined. The steps in the nodal analysis method are:
- Count the number of principal nodes or junctions in the circuit. Call this number n. (A principal node or junction is a point where 3 or more branches join. We will indicate them in a circuit diagram with a red dot. Note that if a branch contains no voltage sources or loads then that entire branch can be considered to be one node.)
- Number the nodes N1, N2, . . . , Nn and draw them on the circuit diagram. Call the voltages at these nodes V1, V2, . . . , Vn, respectively.
- Choose one of the nodes to be the reference node or ground and assign it a voltage of zero.
- For each node except the reference node write down
Kirchoff’s Current Law in the form "the
algebraic sum of the currents flowing out of a
node equals zero". (By algebraic sum we mean that a
current flowing into a node is to be considered a negative
current flowing out of the node.)
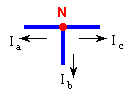
For example, for the node to the right KCL yields the equation:
Ia + Ib + Ic = 0
Express the current in each branch in terms of the nodal voltages at each end of the branch using Ohm’s Law (I = V / R). Here are some examples:-
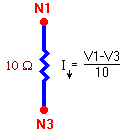 The current downward out of node 1 depends on the voltage
difference V1 - V3 and the resistance in the
branch.
The current downward out of node 1 depends on the voltage
difference V1 - V3 and the resistance in the
branch. 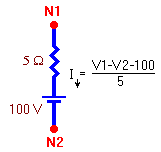 In this case the voltage difference across the resistance is
V1 - V2 less the voltage across the voltage
source. Thus the downward current is as
shown.
In this case the voltage difference across the resistance is
V1 - V2 less the voltage across the voltage
source. Thus the downward current is as
shown.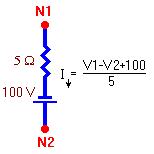 In this case the voltage difference across the resistance
must be 100 volts greater than the difference V1 - V2. Thus
the downward current is as shown.
In this case the voltage difference across the resistance
must be 100 volts greater than the difference V1 - V2. Thus
the downward current is as shown.
The result, after simplification, is a system of m linear equations in the m unknown nodal voltages (where m is one less than the number of nodes; m = n - 1). The equations are of this form:
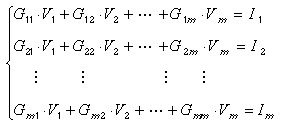
where G11, G12, . . . , Gmm and I1, I2, . . . , Im are constants.
Alternatively, the system of equations can be gotten (already in simplified form) by using the inspection method.
-
- Solve the system of equations for the m node voltages V1, V2, . . . , Vm using Gaussian elimination or some other method.
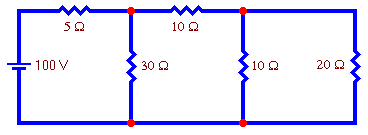
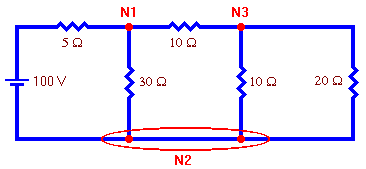
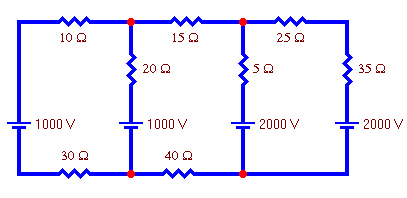
Example 1:
Use nodal analysis to find the voltage at each node of this circuit.