Here we will explain what a system of linear equations is and show how such a system can be solved using the method of Gaussian Elimination.
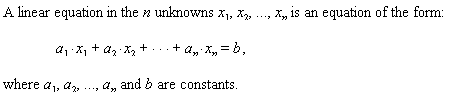
The name linear comes from the fact that such an equation in two unknowns or variables represents a straight line. A set of such equations is called a system. An example of a system of three linear equations in the three unknowns x, y and z is:
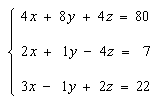
Click here if you wish to see how systems of 2 equations in 2 unknowns can be solved graphically or if you are unfamiliar with the terms redundant and inconsistent.
We will represent a system of equations by a rectangular array of numbers called an augmented matrix. Here is the augmented matrix for the above example:
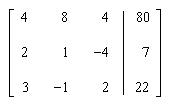
Some Terminology:
- The entries in the augmented matrix are called elements.
- Rows run across the matrix.
- Columns run down the matrix.
- The diagonal of the matrix is the set of elements that starts at the top, left corner and runs diagonally down and to the right. The diagonal of the above matrix consists of the numbers 4, 1 and 2.
- Any elements in position a are said to lie
above the diagonal, and any in position
b are below the diagonal:
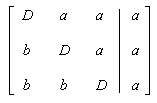
Keep in mind the following:
- the i-th row of the augmented matrix represents the i-th equation
- the j-th column (to the left of the vertical line) represents the (coefficients of the) j-th variable or unknown
- the vertical line represents the equal signs
Solving a System of Equations
Recall that an equation such as:
7(x-4)=14,
may be solved for x by applying the following operations:
- dividing both sides of the equation by the same value, namely 7, to yield x-4=2,
- then adding the same quantity to both sides, namely 4, to yield x=6.
The solution is x=6, as can be verified by substituting it back into the original equation and finding the identity 14=14.
Similarly, the solution of a system of equations is any set of values of all of the variables that satisfies all of the equations simultaneously. For example the system:
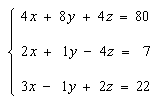
has the solution: {x = 7, y = 5, z = 3}.
This can be verified by substituting these values into all three of the equations and producing three identities.
A system of equations can be solved by generalizing the two operations described above and observing that the solution of a system of equations is not changed by:
- dividing an both sides of an equation by a constant, or
- subtracting a multiple of one equation from another equation.
These same operations can be applied to the rows of an augmented matrix, since each row just represents an equation. They are then called Elementary Row Operations.
The Elementary Row Operations (E.R.O.’s) are:
E.R.O.#1: Choose a row of the augmented matrix and divide (every element of) the row by a constant.
Example:
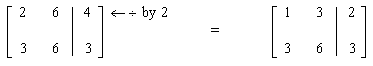
The notation means to divide the first row of the augmented matrix by 2 to produce the new augmented matrix.
E.R.O.#2: Choose any row of the augmented matrix and subtract a multiple of any other row from it (element by element).
Example:
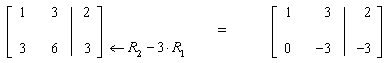
The notation means to take row 2 and subtract 3 times row 1 from it to produce the new augmented matrix.
We will apply the E.R.O.’s in a certain sequence (the Gaussian elimination method, described below) to transform the augmented matrix into triangular echelon form. In this form the augmented matrix has 1’s on the diagonal, 0’s below the diagonal and any numbers above the diagonal. For example, the augmented matrix:
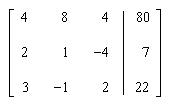
transformed into the triangular echelon form is:
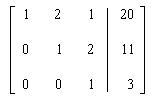
This new augmented matrix represents the system of equations:
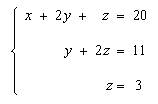
It is solved by back-substitution. Substituting z = 3 from the third equation into the second equation gives y = 5, and substituting z = 3 and y = 5 into the first equation gives x = 7. Thus the complete solution is:
{x = 7, y = 5, z = 3}.
Click Here to Continue