In the Gaussian Elimination Method Elementary Row Operations (E.R.O.’s) are applied in a specific order to transform an augmented matrix into triangular echelon form as efficiently as possible.
This is the essence of the method: Given a system of m equations in n variables or unknowns, pick the first equation and subtract suitable multiples of it from the remaining m-1 equations. In each case choose the multiple so that the subtraction cancels or eliminates the same variable, say x1. The result is that the remaining m-1 equations contain only n-1 unknowns (x1 no longer appears).
Now set aside the first equation and repeat the above process with the remaining m-1 equations in n-1 unknowns.
Continue repeating the process. Each cycle reduces the number of variables and the number of equations. The process stops when either:
- There remains one equation in one variable. In that case, there is a unique solution and back-substitution is used to find the values of the other variables.
- There remain variables but no equations. In that case there is no unique solution.
- There remain equations but no variables (ie. the lowest row(s) of the augmented matrix contain only zeros on the left side of the vertical line). This indicates that either the system of equations is inconsistent or redundant. In the case of inconsistency the information contained in the equations is contradictory. In the case of redundancy, there may still be a unique solution and back-substitution can be used to find the values of the other variables.
Examples of all these possibilities are given below.
Algorithm for Gaussian Elimination:
Transform the columns of the augmented matrix, one at a time, into triangular echelon form. The column presently being transformed is called the pivot column. Proceed from left to right, letting the pivot column be the first column, then the second column, etc. and finally the last column before the vertical line. For each pivot column, do the following two steps before moving on to the next pivot column:
- Locate the diagonal element in the pivot column. This element is called the pivot. The row containing the pivot is called the pivot row. Divide every element in the pivot row by the pivot (ie. use E.R.O. #1) to get a new pivot row with a 1 in the pivot position.
- Get a 0 in each position below the pivot position by subtracting a suitable multiple of the pivot row from each of the rows below it (ie. by using E.R.O. #2).
Upon completion of this procedure the augmented matrix will be in triangular echelon form and may be solved by back-substitution.
Example: Use Gaussian elimination to solve the system of equations:
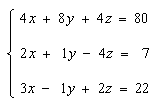
Solution: Perform this sequence of E.R.O.’s on the augmented matrix. Set the pivot column to column 1. Get a 1 in the diagonal position (underlined):
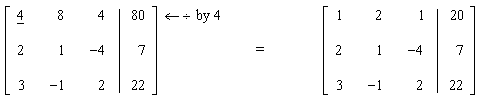
Next, get 0’s below the pivot (underlined):
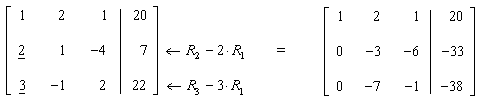
Now, let pivot column = second column. First, get a 1 in the diagonal position:
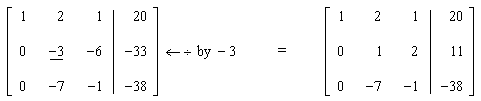
Next, get a 0 in the position below the pivot:
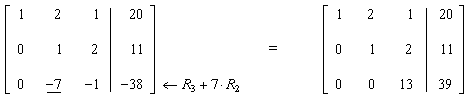
Now, let pivot column = third column. Get a 1 in the diagonal position:
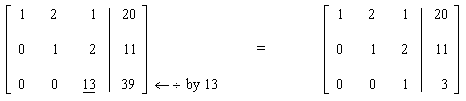
This matrix, which is now in triangular echelon form, represents:
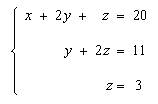
It is solved by back-substitution. Substituting z = 3 from the third equation into the second equation gives y = 5, and substituting z = 3 and y = 5 into the first equation gives x = 7. Thus the complete solution is:
{x = 7, y = 5, z = 3}.
More Topics:
- Example of Gaussian Elimination Applied to a Redundant System of Linear Equations
- Example of Gaussian Elimination Applied to an Inconsistent System of Linear Equations
- Download Software to do Gaussian Elimination