Use Gaussian elimination to put this system of equations into triangular echelon form and solve it if possible:
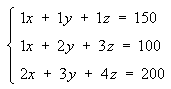
Use Gaussian elimination to put this system of equations into triangular echelon form and solve it if possible:
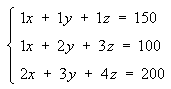
Perform this sequence of E.R.O.’s on the augmented matrix. Set the pivot column to column 1. There is already a 1 in the pivot position, so proceed to get 0’s below the pivot:
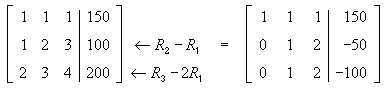
Now, set the pivot column to the second column. There is already a 1 in the pivot position, so proceed to get 0’s below the pivot:
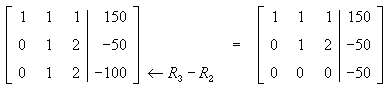
Now, set the pivot column to the third column. The first thing to do is to get a 1 in the diagonal position, but there is no way to do this. In fact this matrix is already in triangular echelon form and represents:
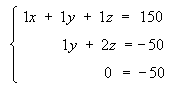
This system of equations is inconsistent and has no solution. The last equation states a contradiction, namely 0 = -50.
In general, an augmented matrix which has been put into triangular echelon form and which contains one or more bottom rows consisting of all zeros to the left of the vertical line and a non-zero number to the right indicates an inconsistent system of equations with no solution.
Written by Eric Hiob, Tuesday, December 31, 1996