The graphical method is not very useful as a computational tool but it is useful for visualizing concepts such as the uniqueness of the solution or the meaning of inconsistent or redundant systems. Consider the following system of two linear equations in two unknowns:
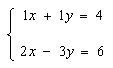
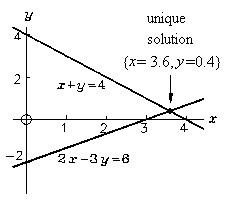
In this method we simply draw graphs of the equations as we have done to the right. Notice that the graph of each equation is a straight line. (This is the hallmark of a linear system. There are no curves, only straight lines.)
Any point on one line is a solution of one equation and any point on the other line is a solution of the other equation. The point where the lines cross {x=3.6,y=0.4} is the solution that satisfies both equations simultaneously. Notice that the solution is unique. This is because the lines are straight and there is only one point where they can cross.
A system of linear equations with a unique solution is the "normal" situation. However it is possible to have a system of equations with no solution. Such a system of equations is called inconsistent. It is often the result of an inaccurate or incorrect analysis of the physical system being described by the system of equations.
Consider the following system of two linear equations in two unknowns:
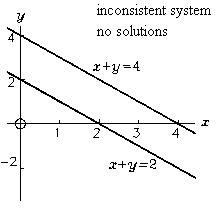
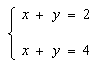
This system of equations is inconsistent because there is no way that x+y can equal 2 and 4 at the same time. The figure to the right shows that the graph of this system consists of two parallel lines that never cross. Thus there is no solution.
It is also possible to have a system of equations with an infinite number of solutions. Such a system of equations is called inconsistent or redundant, respectively. It is the result of an incomplete analysis of the physical system.
Consider the following system of equations:
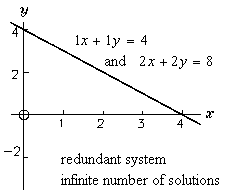
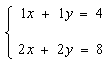
This system is redundant because the second equation is equivalent to the first one. The graph consists of two lines that lie on top of one another. They ‘cross’ at an infinite number of points, so there are an infinite number of solutions.
To summarize, a linear system with 2 unknowns must have at least 2 equations to get a unique solution. Having 1 equation is not enough, because 1 equation in 2 unknowns is represented by an entire line. Having 2 equations is exactly enough, as long as they are not redundant or inconsistent. Having 3 (or more) equations is too many. The third equation must be either redundant or inconsistent.
These ideas can be generalized to linear systems of equations with more unknowns:
“A linear equation in n variables represents a "hyperplane" in an n dimensional space. A linear system of equations with n unknowns must have at least n equations to get a unique solution. Having any fewer is not enough; the solution will not be unique. Having n equations is exactly enough, as long as they are not redundant or inconsistent. Having any more than n equations is too many; the system will be either redundant or inconsistent.”