Geomatics: Vertical Curves Design Using Integrals

Background:

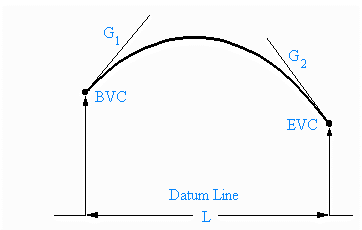
Vertical curves for roads are often designed under certain conditions which lead to the curves having a vertical, parabolic cross-section. In laying out these curves surveyors use four design parameters to determine the coefficients a,b and c. Looking at the diagram these four values can be explained. The first one is the elevation above the datum line at BVC, the beginning of the vertical curve; the second is the grade (G1) of the road at BVC i.e. the slope of the tangent to the parabola at BVC; the third is the grade (G2) of the road at EVC, the end of the vertical curve; and the last is the horizontal length (L) of the curve from BVC to EVC. G1 and G2 are usually expressed as % grades. These grades are often posted at the roadside at the beginning of steep hills. The conditions under which the curves are designed are:

  1. The rate of change of the slope of the curve over the length of the curve must be constant.
  2. The slope at the beginning of the curve must be the same as the slope of the road section joining the curve.
  3. The elevation of the road at the beginning of the curve must be the same as the elevation of the road section to which it is joined. For ease of notation the elevation will be named BVC.

Problem:

Find the equation of the curve given these three conditions.

Solution:

Consider the first condition. The rate of change of slope of a curve is given by

In this case the slopes at two points are known and the distance between the points is also known. The slope of the curve at BVC is G1 and the slope of the curve at EVC is G2. The change in the slope between these points is G2 - G1 and the average rate of change of slope is found by dividing the change by the distance between the points. But this rate of change is constant by the design criteria so we can set up the relation:

Remember that grades are % grades. Integrating gives

=

The second condition tells us that at x = 0 the slope of the curve is the same as the slope of the section of road joining the curve. So, at x = 0

Therefore:

which gives

So,

Integrating gives

=

The third condition shows that, at x = 0, y = BVC. Substituting in the equation gives K2 = BVC.

So the equation of the vertical curve is a parabola of the form:

Actually this result is the starting point of another application in our table of examples, namely, how linear algebra is used in surveying

Return To Math ApplicationsPage

Written by Colin Lawrence, June 26, 1998