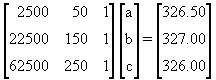Geomatics: Determining Parabolic Vertical Curves for Roads

Background

Vertical curves for roads are often designed to have a vertical, parabolic cross-section. The mathematical form of these curves is the customary parabolic form y = ax2 + bx + c.

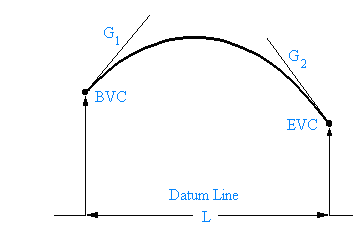
In laying out these curves surveyors use four design parameters to determine the coefficients a,b and c. Looking at the diagram these four values can be explained. The first one is the elevation above the datum line at BVC, the beginning of the vertical curve; the second is the grade (G1) of the road at BVC i.e. the slope of the tangent to the parabola at BVC; the third is the grade (G2) of the road at EVC, the end of the vertical curve; and the last is the horizontal length (L) of the curve from BVC to EVC. G1 and G2 are usually expresses as % grades. These grades are often posted at the roadside at the beginning of steep hills.

Knowing a little of the geometry of the parabola it is relatively easy to show that

and c = elevation at BVC

so that the equation of the parabola becomes

Question

A vertical curve of horizontal length 300m passes through the three points given below where horizontal distance is measured from BVC and elevation is height above the datum line.

x = 50m, y = 326.50m

x = 150m, y = 327.00m

x = 250m, y = 326.00m

Find the elevation at BVC, G1, G2, and the maximum elevation of the curve.

Solution

Substitute the three sets of coordinates into y = ax2 + bx + c giving this set of equations

326.50 = a(50)2 + b(50) + c

327.00 = a(150)2 + b(150) + c

326.00 = a(250)2 + b(250) + c

or simplifying

2500a + 50 b + c = 326.50

22500a + 150b + c = 327.00

62500a + 250b + c = 326.00

or putting into matrix form

Solving gives a = -0.000075, b = 0.02 and c = 325.6875.

So the equation of the parabola is y = -0.000075x2 + 0.02x + 325.6875. Now compare this to the equation for the parabola that was given above, namely

Obviously BVC = 325.6875m . Next compare the coefficients of x

so G1 = 2% .

Now compare the coefficients of x2

.

Knowing that L = 300m it is easy to find G2 = -2.5%.

The parabola has a maximum at

Substituting this value of x into the equation for the parabola gives

y = -0.000075(133.333)2 + 0.02(133.333) + 325.6875 = 327.021m.

So the curve has a maximum elevation of 327.021m

Return To Math ApplicationsPage

Written by Colin Lawrence, September 21, 1997