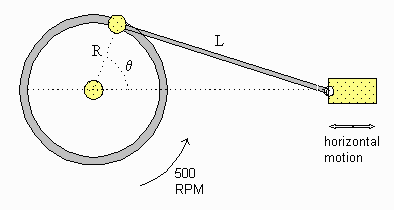
As the flywheel rotates at a constant rate of 500 rpm, the piston moves back and forth along a horizontal line. If R = 10 cm and L = 40 cm then what is the linear velocity of the piston, when angle θ = 160°?
As the flywheel rotates at a constant rate of 500 rpm, the piston moves back and forth along a horizontal line. If R = 10 cm and L = 40 cm then what is the linear velocity of the piston, when angle θ = 160°?
In the triangle with sides R and L, name the third side (the base) x.
R and L are constant, but x is a function of time, x(t). The desired velocity is dx/dt.
Apply the Cosine Law:
L2 = R2 + x2 - 2 R x cos θ [equation 1]
Recalling that θ and therefore x are functions of time, perform implicit differentiation:
0 = 2x dx/dt - 2R [ dx/dt cos θ- x sin (θ) dθ/dt ] [equation 2]
To use this equation to find dx/dt, we need R, θ, dθ/dt, and x.
402 = 102 + x2 - 2 (10) x (-.9397)
This becomes
x2 + 18.79 x - 1500 = 0
The roots are -49.25 and 30.46, and we need the positive root.
Substituting all the values into equation [2] we get:
0 = 2(30.46) (dx/dt) - 2 (10) [ - .9397 dx/dt - 30.46 ( .3420) (52.36)]
(-60.92 - 18.79) dx/dt = 10909
dx/dt = -136.9 cm/sec
The negative sign indicates that x is getting smaller, which is correct when θ < 180°
Written by Val Sawadsky, October 7, 1997