Prosthetics: Forces Acting on a Femur

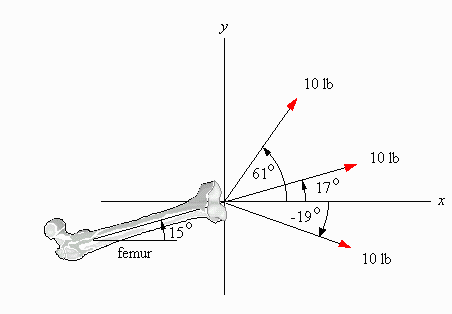
Solution

In order to determine the resultant force R, which is a vector, we have to calculate both its magnitude and its direction. First, let us compute the magnitude of R. We accomplish this by resolving each force into its x and y components, and then summing up all the x components and summing up all the y components as follows:

Force	x-component	y-component
F1 = 10 lb	10 cos(-19°) = 10 × 0.9455 = 9.455	10 sin(-19°) = 10 ×(-0.3256) = -3.256
F2 = 10 lb	10 cos(17°) = 10 × 0.9563 = 9.563	10 sin(17°) = 10 × 0.2924 = 2.924
F3 = 10 lb	10 cos(61°) = 10 × 0.4848 = 4.848	10 sin(61°) = 10 × 0.8746 = 8.746
Resultant R	Rx = 23.866	Ry = 8.414

Since we have calculated the x and y components of the resultant R, we can find its magnitude by using the Pythagorean theorem:

R2 = Rx2 + Ry2 = 23.8662 + 8.4142 = 569.586 + 70.795 = 640.381

which gives us:

R = 25.306 or rounded to 2 significant digits, the same as the original measurements: R = 25 lb.

The angle of the resultant can be calculated as follows:

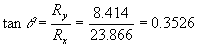
From this:

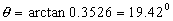
Since the femur had an original orientation of 15° we can conclude that the effect of this traction system on the femur will be a rise of 4.42°.

---