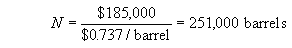Petroleum: Statistical Control of Oil Barrel Filling

A machine fills 45 gallon barrels with diesel motor oil with a standard deviation of 0.302 gallons/barrel. According to consumer laws, at least 90% of the barrels must have at least 45 gallons in them.

  1. What fill amount must the machine be set at to ensure 90% have at least 45 gallons? Assume a normal distribution for the actual amount of oil in each barrel.

  2. If an attachment to the machine, costing $185,000, will cut the standard deviation to 0.093 gal/barrel, and the wholesale price of the oil is $2.75/gal, how many barrels must be filled to break even on the attachment investment?

Solution:

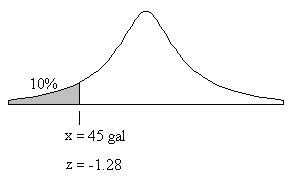
  1. The diagram shows a normal distribution describing the actual fill amounts. We must find the mean fill μ (ie. the location of the peak) which would result in a fill of less than 45 gallons only 10% of the time. To do this we transform our normal distribution to the standard normal distribution using this change of variable

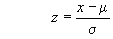
    where z is the standard normal variable whose distribution is given in tables, x is the 45 gallon fill per barrel in question, μ is the mean fill per barrel (unknown), and σ is the standard deviation of the fill per barrel. The standard normal distribution table shows that 10% of the area of the normal curve lies below the value z = -1.28. Solving for μ gives

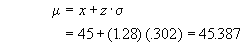
    Thus the mean fill must be set at 45.387 gallons/barrel.

  2. Begin by finding the fill μ which would result in a fill of less than 45 gallons only 10% of the time with the new attachment. Using the new numbers

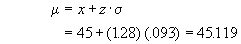
    This means that the machine can be set at 45.119 gallons/barrel rather than the previous 45.387 gallons/barrel. This is a saving of 0.268 gallons/barrel or a savings of $0.737/barrel. The number of barrels required to pay for the machine is

Return To Math ApplicationsPage

Written by Graham Cocksedge, September 21, 1997