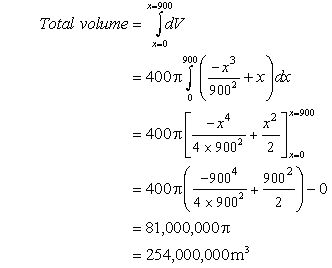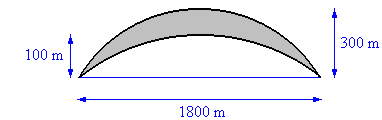
Pools of oil collect in underground domes. Find the volume of the dome of oil enriched strata shown in cross section in the diagram. The upper and lower boundaries are both paraboloids and the dome is circular in plan (when viewed from above).
Pools of oil collect in underground domes. Find the volume of the dome of oil enriched strata shown in cross section in the diagram. The upper and lower boundaries are both paraboloids and the dome is circular in plan (when viewed from above).
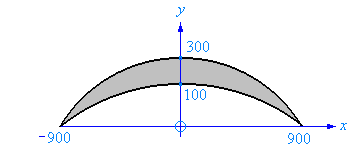
The dome’s upper and lower boundaries are both parabolas when viewed in cross-section. If we place each parabola’s axis of symmetry on the y axis then each parabola is of the form
y = a x2 + b,
where b is the y intercept and a is a negative number.
a can be found by using the fact that the point (900,0) is on both parabolas.
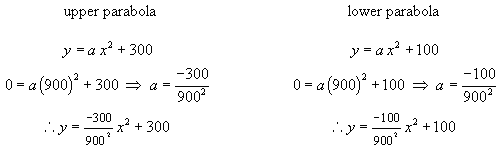
The result is the equation for each parabola. To find the area of the dome imagine breaking it up into elemental rings as shown to the right. The volume of each ring is
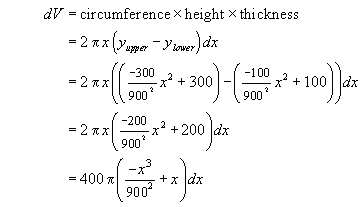
The total volume of the dome is found by integrating over all of the elemental rings
Written by Graham Cocksedge, September 21, 1997