This example is adapted from an article on "Monitoring
Radioactive Xenon Gas in Room Air Using Activated Charcoal",
Journal of Nuclear Medicine Technology, March 1990.
The purpose of the study was to investigate the use of
activated charcoal as a means of monitoring radiation exposure to
the staff while performing Xenon-133 studies. Xenon-133 is widely
used for brain and blood flow measurements. It is exhaled by
patients during the study. The expired Xenon -133 must be
contained by a face mask or vented to the atmosphere without
exposing the technologist performing the evaluation.
Part of the study involved setting up a reference standard
from which efficiency of the adsorption onto activated charcoal
could be judged.
111 MBq of Xenon-133 was heat sealed into a tube and the exact
amount of radioactivity was measured in a dose calibrator
periodically for 31 days. The results are as shown:
Xenon-133 Standard Decay in Dose
Calibrator
time t
(days)
|
Activity A
(% of Initial Measured Activity)
|
|
0
|
100
|
|
5
|
51.7
|
|
11
|
23.5
|
|
15
|
13.8
|
|
18
|
9.2
|
|
21
|
6.3
|
|
24
|
4.4
|
|
32
|
1.5
|
Here is a graph of the above data. Notice that the vertical axis
has been logged.
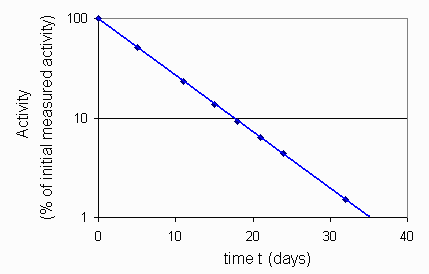
Problem:
Find an equation containing no logarithms to represent this
observed data. Be sure and identify any transformations you may
have applied to the independent and dependent variables.
Solution:
Technical Notes:
- Nuclear Medicine technologists would know that radioactive
decay has an exponential relationship, typically given by:
A = A0e-λ t (equation 1)
where λ and Ao are constants. Our job in this case
is to solve for Ao
and λ.
- If you log or ln (natural logarithm) both sides of an exponential equation such as that shown in equation (1), you
get a linear equation.
Let x represent the time t (in days)
and y represent the
natural logarithm of the % of initial measured activity,
ln(A).
These are the transformations we will apply to the data to solve
for the two constants.
Then using the formula for a straight line, y = bx + a and
applying the transformations, we get a linear equation, ln(A) = bt + a.
Now to solve for b and a,
- you can get an approximate "eyeball" answer by
picking any two points off the graph of the line shown. For
example, you might pick values (21, 6.3) and (5, 51.7) which
could then be substituted for t and A into the
equation for a straight line giving two equations in two unknowns to
solve.
ln(6.3) = 21b + a
ln 51.7 = 5b + a
Subtracting the second equation from the first and using our
calculator on the logs we get:
-2.104908 = 16 b
b= -0.131556759
Substituting into the first equation and solving for a gives
a = 4.603241578
Thus the equation becomes
ln(A) = -0.13156 t + 4.60324
you can also use the preferred method which is to apply the
method of Least Squares to the data. This is a built in
function on most calculators. In this case,
b = -0.130992968, a = 4.598029229
Now we still have the problem of expressing the equation so
that it contains no logarithms.
ln A= -0.13156 t + 4.60324
Antilog, recalling that:
ax + y = ax · ay
This gives our final answer:
A = e-0.13156 t + 4.60324 = e-0.13156 t · e4.60324 = 99.8 e-0.13156 t
