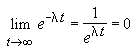In the September 1986 edition of the Journal of Nuclear Medicine Technology an article appeared on "An Integration Technique for Rapid Estimation of Activity of Waste in Storage". One of the problems hospitals face is disposing of radioactive wastes. An increasingly popular method is to allow radionuclides with short half-lives to decay at the hospital until they can be disposed of as nonradioactive waste (after about 10 half-lives of the radioactive nuclide have elapsed.). This is a cheaper method of disposal and reduces the volume of low-level radioactive waste sent to shallow-land burial sites.
However, radioactive wastes held in storage contribute to the overall activity which is in the user’s possession. Since there are limits on the amounts of various radioactive nuclides that can be possessed, a method for determining the activity of radoactive wastes held in storage is needed. The following method overestimates the activity in storage which results in a conservative restriction on activity on hand in the laboratory.
In a facility where the usage rate of a radionuclide is well defined and relatively constant, the total activity, A, of this radionuclide held in storage at any time, t, can calculated. The rate of change in activity as a function of time, dA/dt, is expressed as the difference between the rate at which waste is placed in storage and the rate of decay:
where:
- R is usage rate of the radionuclide (its units are
activity/time),
- f is the fraction of the used activity in the
facility which is transferred to storage (no units)
- λ is the decay constant of the radionuclide (its units are 1/time)
Problem:
- Determine an equation for the activity A in terms of the time t if initially A = 0.
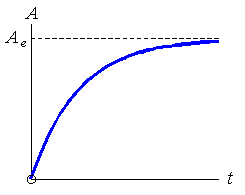
- The activity accrued in storage increases as a function of time. However, as time becomes large, the activity approaches an equilibrium value Ae. Find this equilibrium value Ae that A approaches.