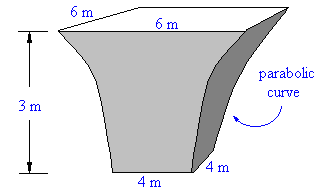
To avoid stress concentrations, tunnels and support pillars should be rounded. Find the volume of the square cross-section pillar shown to the right.

To avoid stress concentrations, tunnels and support pillars should be rounded. Find the volume of the square cross-section pillar shown to the right.
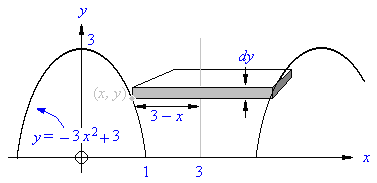
We will use the geometry shown to the right. We will place the parabola forming the left edge of the pillar with its axis of symmetry on the y axis and its vertex at y = 3. The first step is to find the equation of this parabola. The parabola must have the form:
y = a x2 + b,
where b is the y intercept (= 3) and a is a negative number.
a can be found by using the fact that the point (1,0) is on the parabola:
y = a x2 + b,
y = a x2 + 3,
0 = a (1)2 + 3,
a = - 3,
Thus the equation of the parabola is:
y = - 3 x2 + 3.
The second step is to use this formula to find the dimensions of the elemental rectangular slab shown in gray in the picture above. The slab has its edge located at (x, y). To find x, solve the above equation for x:
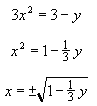
Thus the volume of the rectangular slab element shown in gray is:
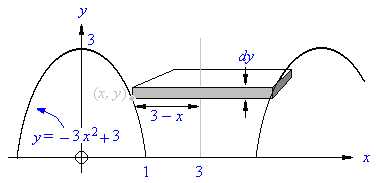
Integrating over all the elemental slabs from y = 0 to y = 3 gives the entire volume of the pillar:
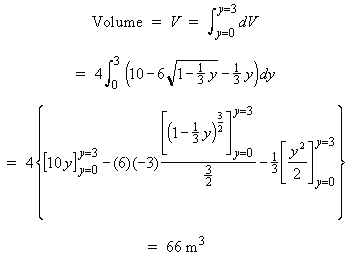
The volume of the pillar is 66 m3