BCIT ~ Mathematics - Examples - Mechanical Engineering Technology

Question

An inspection sampling plan is set up to randomly sample 4 meters from a roll of 220 meters of plastic coated wire and to accept the wire roll if no flaws are found in the 4 meter length. What is the probability that a wire roll with an average of 0.8 flaws per meter will be rejected by the plan?

Solution

The solution to this problem requires a knowledge of the Poisson Probability Model and of the rules of probability:

The Poisson Probability Model says that the probability of finding exactly x flaws in a fixed length of wire is given by :
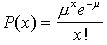
In this formula, μ= the mean number of flaws = 0.8 flaws / meter = 3.2 flaws / 4 meters,
and x! denotes the factorial function.
The complement rule for probability says:
P(A will happen) = 1 - P(A won’t happen)

Applying the Poisson Probability Model:

P(0 flaws) = P(accept the roll using the sampling plan) =

Applying the complement rule:

P(reject the roll using the sampling plan) = 1 - P(0 flaws) = 1 - 0.0408 =0.9592

There is a 96% chance that a roll with as many as 0.8 flaws/meter will be rejected by this sampling plan.

Mechanical: Predicting Probability of Manufacturing Flaws

Question

Solution