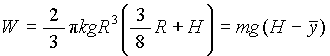Solutions
- The volume
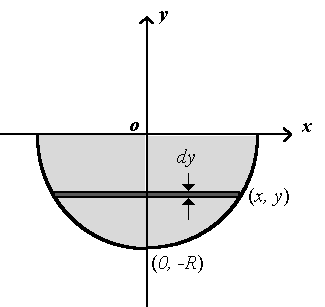
We consider the hemisphere as the solid obtained by rotating the fourth quadrant of the curve x2+y2=R2 about the y-axis. Through a point (x, y) on the curve we draw a circular disk perpendicular to the y-axis as our volume element dv . The radius of the disk is x and the thickness is dy, and consequently,
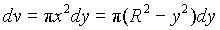
Therefore, the total volume of the hemisphere is:
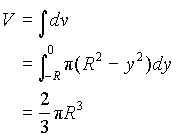
- The y-coordinate of
the centroid
We can use the same infinitesimal volume element dv in (a). Since dv is a disk perpendicular to the y-axis, the y-coordinate of any point in the disk is y. Therefore,
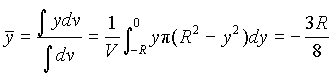
- The moment of inertia about the
y-axis.
To find the moment of inertia about the y-axis, we need to choose another volume element dv such that the distance from the y-axis to any point in dv will be the same. A convenient choice is a thin-walled cylindrical shell centred at the y-axis, as shown in the figure below. From the figure we can identify the radius, the height, the thickness and the volume of the cylindrical shell:
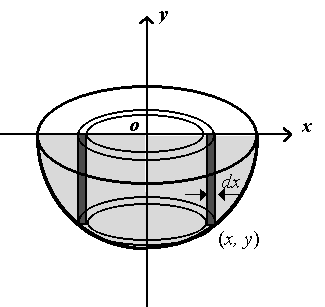
radius = x ;
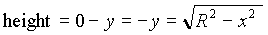
thickness = dx .
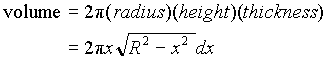
The moment of inertia of the shell is:
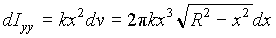
where k is the density of water. Therefore, moment of inertia of the water in the hemispherical tank is given by:
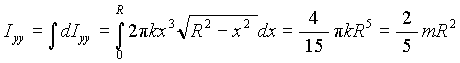
- The work needed to pump all
the water to a height of H metres above the top of the
tank.
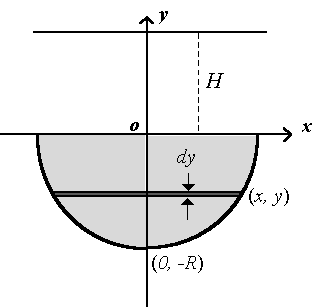
From physics we know that the work needed to lift a particle by a vertical distance h is mgh, which is the increase in potential energy. Then, the element of volume should be chosen such that all the points in the element are at the same height. Therefore, we can choose a horizontal disk as our volume element, same as that used in (a):
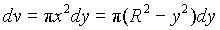
This volume element must be lifted a vertical distance (H - y), and the work for it is
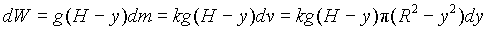
Then, we can integrate dW and find the total work needed to pump all the water:
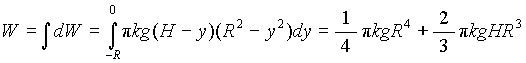
Or,