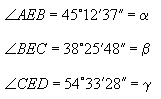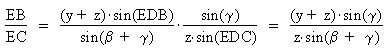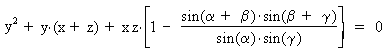
One problem encountered in Surveying is:
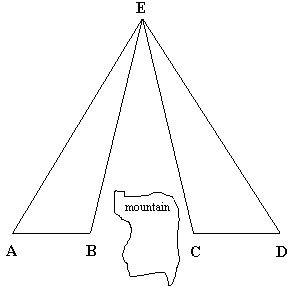
How do you find the length of the baseline AD when it is interrupted by an obstacle? The obstacle in question is a mountain that the surveyor cannot see through. The surveyor knows that each measurement costs money so she decides to minimize the number of measurements she has to make. The following observations were made:
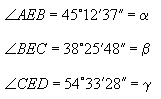
Length AB = 436.3m = x
Length BC = ? = y, and
Length CD = 542.8m = z.
Two pairs of triangles are considered in turn: first ΔEAB and ΔECA; next ΔEBD and ΔECD.
In ΔEAB
In ΔEAC
EB and EC both contain an angle that has not been measured and about which there is no information. However, by finding the ratio EB:EC that can be resolved.
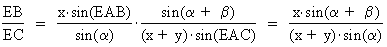
Next consider ΔEBD and ΔECD. The same reasoning for these two triangles shows that
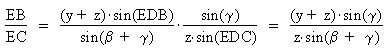
Thus,
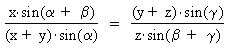
The only unknown in this equation is y, the distance BC through the mountain. The equation can be rearranged into a quadratic equation in y.
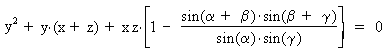
By plugging in the given values two roots are found for y.
y1 = 150.26 m and y2 = -1129.36 m
The solution is obviously 150.26m but why is y2 equal to the magnitude of AD?
Written by Colin Lawrence, October 10, 1997