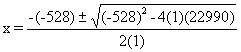Surveyors have the responsibility of subdividing regular or irregular shaped lots into areas of equal size. Here is a simple example. A trapezoidal lot with bases 60m and 35m and perpendicular depth 110m must be subdivided into two equal-size lots by a line parallel to the bases. What is the distance (call it x) from the 60m base to this line?
Recall the formula for the area of a trapezoid
A = (1/2)(b1 + b2)h.
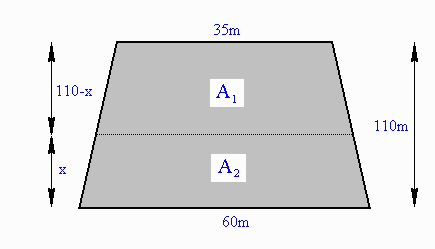
where b1 and b2 are the base lengths and h is the perpendicular height of the trapezoid. Thus the area of the original trapezoid is
A = (1/2)(35m + 60m)(110m) = 5225 m2 .
Let x = perpendicular height from the 60m base to the dividing line.
Let y = length of the subdividing line.
Then the area of the lower trapezoid is
A2 = (1/2)(60 + y)x
and we know that A2 = (1/2)A, so (1/2)(60 + y)x = (1/2)5225 giving
(60 + y)x = 5225. (Equation 1)
We know also that A1 = (1/2)A, so (1/2)(35 + y)(110 - x) = (1/2)5225 giving
(35 + y)(110 - x) = 5225. (Equation 2)
From equation (1)
60 + y =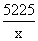 
Substituting in (2) gives
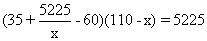
Multiplying by x and rearranging we get
(5225 - 25x)(110 - x) = 5225x
574750 - 7975x + 25x2 = 5225x
25x2 - 13200x + 574750 = 0
which leads to the quadratic
x2 - 528x + 22990 = 0.
Using the quadratic formula we get
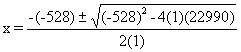
So x = 47.88m or x = 480.12m.
The second root does not work. So, the perpendicular distance from the base to the subdividing line is 47.88m.
Written by Colin Lawrence, June 26, 1998