Goober Island has an area of 109 hectares. Logging and conservation concerns require that we know how many trees are on this wooded island. The island is much too large to count every tree. What can we do?
Goober Island has an area of 109 hectares. Logging and conservation concerns require that we know how many trees are on this wooded island. The island is much too large to count every tree. What can we do?
One solution is to count the trees on a small portion of the island and then estimate the total for the whole area. For example, suppose the count of trees on an 8 hectare section of the island is 621. Then the number of trees per hectare is 621/8 = 77.625. An estimate of the number of trees on the entire island is 77.625 x 109 = 8461.
In mathematical terms, let
Let the actual number of trees on the whole island be T. This won’t be known exactly unless we count every tree on the whole island. However, T can be estimated by
We first compute 
to estimate the number of trees per hectare, and then multiply this by A to
estimate the number of trees on the whole island.)
This raises some questions. How accurate will our estimate,
, be? In other words, how close will be to
T? For example, if we happen to count in an area which
is less heavily treed than the rest of the island, then would
be too low. Is there a better way?
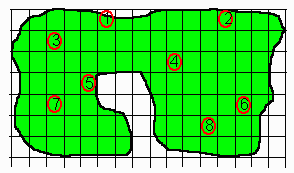
Instead of counting all the trees in one area, we can divide the entire island into small rectangular plots as in the diagram on the right. Then choose some of the plots and count the trees only on those plots. Suppose each of our plots is 1.30 hectares.
In the above diagram, we have chosen 8 plots on which to count trees. The plots must be chosen in a random manner, i.e. every plot on the island must have the same chance of being chosen. By doing this we distribute the area where we are going to count over the island, and this leads to the sample being more representative of the whole island. In fixmewith a symbols, we signify the number of plots on which trees are counted by the letter n. This is called the sample size. Let
We write Σxi to indicate the sum of the xi’s on the n sampled plots.
We write 
to indicate the average of these
xi’s, given by the
formula:
Each plot has an area a, so the
number of trees/hectare on the sampled plots is 
. A good estimate ,
, of the
total number of trees, T, on the entire island (which
has area = A) is
We still have the question: How accurate is this estimate?
The accuracy involves the computation of a quantity called the standard deviation,
The smaller the value of s, the more
accurate the estimate will be. Statistical theory tells us that
for large samples, we can be about 95% sure that
the difference between the mean count on all plots on the island, μ
(includes both those which were sampled and those
which were not), and the mean on the sampled plots, 
, will be less than
, i.e.
that μ will be between 
and 
.
Since our estimate of T is 
, we are
95% sure that T is between
and 
.
On Goober Island, the count of trees on the 8 one-hectare plots are as follows:
362, 422, 486, 513, 368, 405, 334, and 289.
The results of the analysis of this data are:
Our conclusions are:
The best estimate of T, the number of trees on the
entire island, is 
or 33,000 (rounded to the nearest thousand).
We are 95% sure that T is between
and 
, or between 29,000 and 38,000 (rounded to
the nearest thousand).
The above analysis is approximate. We have not allowed for the facts that:
Written by G. John Smith, September 16, 1997