Forestry: Mosse Population and Exponentials

Solution:

Problems such as this can be solved using logarithms and exponentials.

Question 1: What is the average annual rate of growth?

Setting up the problem - translating from words to symbols:

1. Since we want to know the rate of growth of the population, let r be the average annual rate of growth in the population.
2. The population after one year will be P1 = 325 + 325r = 325(1+r).

   After two years it will be P2 = P1 + P1r = 325(1+r) + 325(1+r)r = 325(1 + r)2

   After five years it will be P5 = 325(1 + r)5.

3. After five years we are told the population is 450. Therefore: 325(1 + r)5 = 450.

Solving the equations

1. 
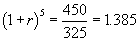
2. Take the fifth root of each side of the equation:

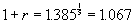
   and hence r = 0.067.

Therefore, the average annual rate of growth is r = 0.067 = 6.7%

---

Question 2: How many years will it take for the population to grow from 450 to 750

Setting up the problem - translating from words to symbols:

1. Let x be the number of years to grow from 450 to 750
2. The annual growth in the population is 6.7%. Another way of saying this is that each year, the population is 1.067 times what it was the previous year. After x years it will be 1.067x times as large. So we can say that:

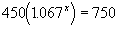
Solving the equation

1. Dividing by 450,
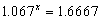
2. Take logarithms of each side. It doesn’t matter what base we use. For this problem let us use 10 as our base.

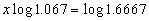
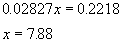
Therefore, it will take 8 years before the poulation reaches 750.

(After 7 years it will not have reached 750, and since there are births only at one time during the year, the population will not reach 750 until 8 years later.)

---