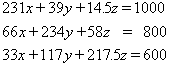My logging company has a contract with a local mill to provide
1000 m³ of Lodgepole pine,
800 m³ of spruce, and 600
m³ of Douglas fir logs per month. I have
three regions available to me for logging. The following table
gives the species mix, and timber density for each
region.
|
Region
|
Volume/hectare
|
% Pine
|
% Spruce
|
% Fir
|
|
West
|
330 m³ / ha
|
70 %
|
20 %
|
10 %
|
|
North
|
390 m³ / ha
|
10 %
|
60 %
|
30 %
|
|
East
|
290 m³ / ha
|
5 %
|
20 %
|
75 %
|
How many hectares should I log in each operating region listed
above to deliver exactly the required volume of logs? I
don’t want to have to store logs so I don’t want
any left over at the end of each month, but I do need to make my
quota.
Solution:
Problems such as this can be solved using simultaneous
equations by identifying quantities we need to know and then
finding relationships between them.
Setting up the problem - translating from words to symbols:
- Since we want to know the number of hectares that should be
logged in each region, start by letting
- x = number of hectares logged in
West region
- y = number of hectares logged in
North region
- z= number of hectares logged in
East region
- The total volume of wood logged in West region
will be the volume of logs / hectare times the
number of hectares, or (330 m3/ha)(xha) =
330xm3.
- The total volume of Lodgepole pine logged in the West
region is the total volume of wood times the
percentage of pine. Since 70% = 0.7, the
total amount of pine from the West region is
0.7(330x)m3.
- If we follow the same steps as 2 and 3 for the North
region, we get the total volume of Lodgepole pine logged in the
North region is 0.1(390y)m3.
- Doing the same for the East region, we get
0.05(290z)m3.
- Steps 3, 4, and 5 calculate the volume of Lodgepole pine
from the three regions. We know the total lodgepole pine needed
is 1000 m3. So we must have
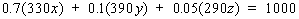
- If the same steps are followed for spruce and Douglas fir,
two more equations will be obtained. These will be
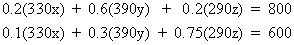
Solving a set of simultaneous equations:
Each equation above contains three unknowns. Let us repeat
these equations and simplify by multiplying out the
numbers:
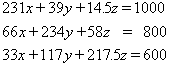
There are many ways to solve for the unknown values x,
y and z. We will consider one way. This is
called elimination. We take pairs of equations and eliminate one
of the variables.
- Solve each of the first two equations for z and
equate them. The result of this procedure is:
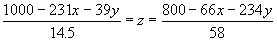
- Solve each of the first and last equations for z
and equate them.
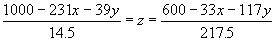
- Remove the z and simplify the equations in 1 and
2.
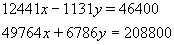We have reduced the problem from one of solving 3 equations
with 3 unknowns to one of solving 2 equations in 2
unknowns
- Let us solve each of the equations in step 3 for y
and equate them.
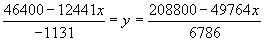
- Remove the y and simplify the equation to
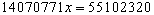
- Solve for x. We get x = 3.92
- Solve for y using one of the equations in step 4.
We get y = 2.05
- Solve for z using any one of the equations in
steps 1 or 2. We get z = 1.06
Answer:
To fulfil the contract we need to log 3.92 hectares in the
West region, 2.05 hectares in the North region and 1.06 hectares
in the East region.
