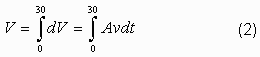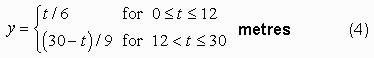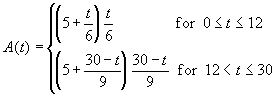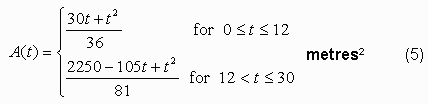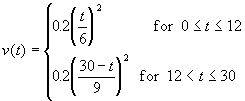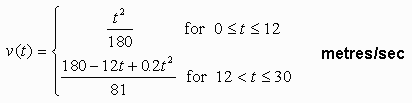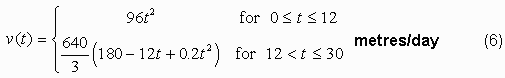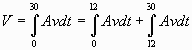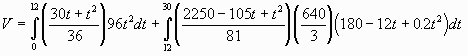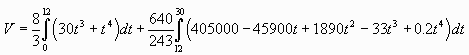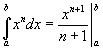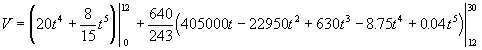During the spring, water levels in rivers rise and flooding
often occurs. To reduce the severity of flooding, sometimes a
flood diversion (or ditch) is built to carry some of the water
during this season.
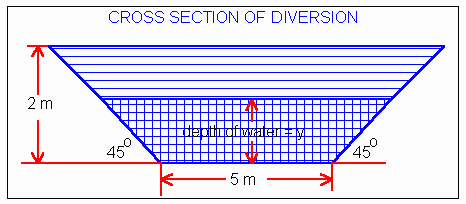
Consider a diversion which is built as in the diagram
below.
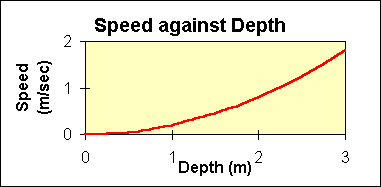
An engineering study has determined that the relationship
between the average speed and depth of water in the diversion in
metres/sec is

This relationship has the following graph.
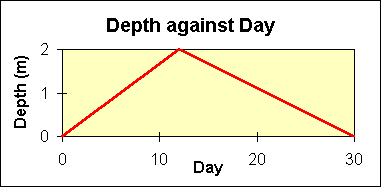
Let us compute the maximum volume of water the diversion can
handle. Suppose excess spring runoff lasts for a month. Water
levels increase for 12 days and then decrease back to normal over
the next 18 days. Suppose at the start (day 0) the water
is just starting to enter the diversion (y =
0). From that time until day 12, the depth
linearly increases to 2m (top of diversion), at which time the
depth peaks. Then the depth linearly decreases, and on day
30, it reaches zero again. In other words, the graph of
depth against time is
QUESTION:
What was the total volume of water that passed through the
diversion during the 30 day period?
SOLUTION:
Step 1: Create an expression for total
volume.
Using calculus, the instantaneous volume passing through a
point in the diversion is
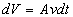
as indicated in the following diagram.
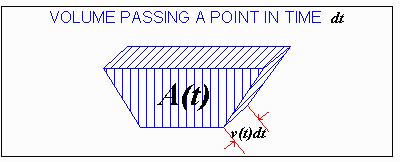
The total volume passing through the diversion during the 30
day period is
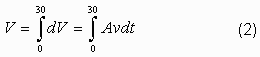
Steps 2 to 6: Compute A and
v as functions of
t.
Step 2: Express A (the
cross-sectional area of water), as a function of
y.
When the depth of water is y, the
cross-sectional area of water is (recall the formula for the
area of a trapezoid, and the geometry of a triangle)

Step 3: Express y as a
function of t.
y increases linearly for
12 days starting at 0m and
ending at 2m. With the formula for a straight
line,
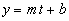
we can use the two points (t = 0, y
= 0) and (t = 12, y =
2) to determine the relationship,
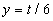
where t is in days and
y is in metres. Starting at day
12, the depth decreases for the next
18 days to zero. As above, we
obtain the formula for a straight line between the points
(t = 12, y = 2) and
(t = 30, y = 0). This line
is
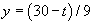
Hence we have
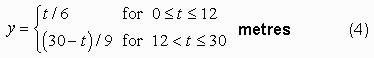
Step 4: Express A as a
function of t.
A is related to y
by equation (3), and y is related to
t by equation (4).
Substituting equation (4) into (3), we obtain
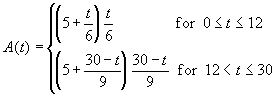
Expanding the brackets:
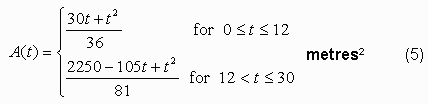
Step 5: Express v as a
function of t.
v is related to y
by equation (1), and y is related to
tby equation (4). If we substitute
equation (4) into (1), we obtain
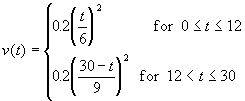
Expanding the brackets:
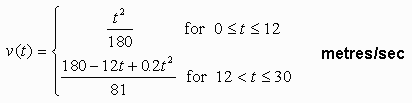
Step 6: Conversion of units.
Notice that the unit of time in the speed,
v, is expressed in
seconds but time everywhere else is expressed in
days. To make the units coincide, let us express
the speed in metres/day.
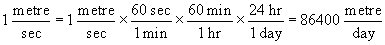
So, the speed expressed in metres/day is
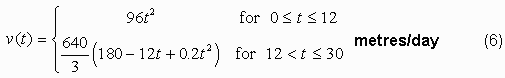
Step 7: Solving the integral.
From equation (2), break the integral into two time periods
since there is a different relationship between
A, v and
t in each of these periods.
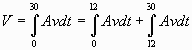
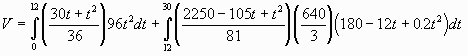
Expanding the brackets and bringing constant factors outside
the integral,
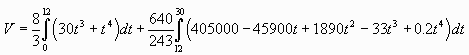
Recall that for any n not equal to
-1,
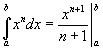
Also, we can integrate an expression one term at a time.
Integrating the expression for V:
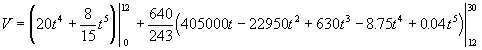
We can now substitute the limits for the unknown,
t, to obtain the answer.
ANSWER:
Evaluating the above expression we get V =
1,368,576 m3 or about
1.37 x 106 m3 passes through the diversion.
This is equivalent to an area 1.17km by
1.17km covered to a depth of
1m.