We are planning to study feeding and growth in mallard ducks
during nesting. We want to build a rectangular enclosure for the
ducks so they will be safe from predators and can be studied.
Also, we want the area of the enclosure to be as large as
possible.
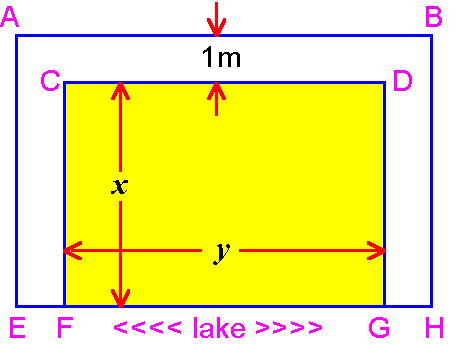
One side of the enclosure is along the straight edge of a lake.
We have 120m of fencing available and need double fencing one
metre apart on the three "land" sides of the enclosure
to keep predators away. On the "water" side, we need
only a single fence (see diagram below - fencing is in
blue).
ENCLOSURE
QUESTION:
To make the area of the enclosure as large as possible,
- What must the dimensions x and
y be?
- What lengths are the seven straight
sections of fence: AB, CD, EH, AE, CF, DG and BH?
- What is the area of the enclosure?
SOLUTION:
Step 1:
Compute the lengths of fence used on
each side in terms of the unknowns x and y.
- Water side (EH):
y+2 metres
- Each side adjacent to the water
side:
Inside fence (CF and DG):
x metres
Outside fence (AE and BH):
x+1 metres
- Side opposite the water side:
Inside fence (CD): y
metres
Outside fence (AB):
y+2 metres
The total length of fencing is 120 metres,
hence
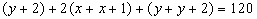
or
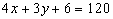(equation 1)
Step 2:
Compute the area of the inside
rectangle in terms of x and y.
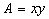(equation 2)
Now solve equation (1) for y
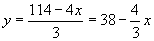(equation 3)
Substitute for y in equation (2). Then,
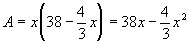
Step 3:
Find the extreme value(s) for area,
A.
A will reach an extreme value (maximum or minimum)
when
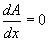
Computing the derivative and setting it to zero,
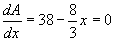(equation 4)
Solving for x,
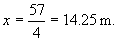
Substituting into equation (3),
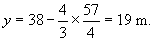
Step 4:
Verify that A has a maximum
at x = 14.25 and not a minimum.
To do this, compute the second derivative,
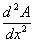
and evaluate at x = 14.25. If
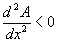
it is a maximum; if
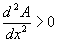
it is a minimum. From (4),
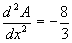
for all x, hence we have a maximum.
ANSWERS:
For the enclosure to have maximum area,
- The dimensions of the inside will be
14.25m by 19m.
- The seven straight sections of fencing
will have lengths:
AB and EH, 21m
AE and BH, 15.25m
CD, 19m
CF and DG 14.25m.
- The area will be 270.75m2.
