Food Technology: Applying Probability and Statistics.

A machine dispensing a somewhat chunky material into packages does not place exactly the same mass in each container. Studies show that the actual mass dispensed each time is an approximately normally distributed random variable with a standard deviation of 15.0 g, and a mean value which can be set at any desired value. At what value must the mean be set to ensure that 90% of the packages contain at least 650 g of material.

Solution:

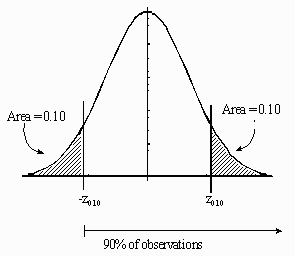
We are asked to find the value of the mean, μ, which will give a 10th percentile equal to 650 g. Standard formulas from the theory of the normal distribution give this as

10th percentile = μ- z0.10 σ,

where -z0.10 is the 10th percentile of the standard normal random variable (which we can determine to be -1.282, from standard normal probability tables), and σ= 15.0 g, the standard deviation.

Solving the above equation for the mean, μ, then gives:

μ=10th percentile + z0.10σ

= 650 g + (1.282)(15.0 g)

= 669.23 g.

Thus, if the mean is set at 670 g, then at least 90% of the containers filled by this machine will have 650 g or more material in them.

Return To Math ApplicationsPage

Written by David Sabo, October 7, 1997