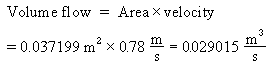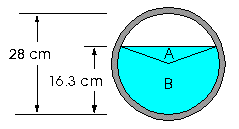
A drainage pipe runs
under the floor of a manufacturing facility. It is circular in
cross-section with an inside diameter of 28 cm as shown to the
right. By inserting a piece of doweling (a stick) in the drain in
the floor, it has been determined that the depth of waste liquid
in the pipe is 16.3 cm. If the rate at which the waste liquid is
flowing to an underground waste facility is 0.78 m/s, determine
how much water flows through the drainage pipe in Imperial
gallons/minute.
Solution:
The first step is to
determine the cross-sectional filled area (shown in blue)
by finding the area of the triangle, A, plus the area of the
sector, B.
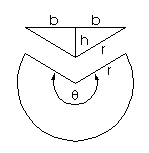
The area of each triangle shown to the
right is given by the formula:

The area of the sector can be found by multiplying the area of
a circle:

by the fraction of a circle that the sector fills. If the
sector’s angle is θ radians, then since a full circle is
2π radians, this area is:
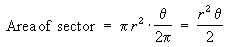
Thus the total area is:
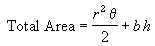
The second step is to find r, h, b and θ from the information provided and evaluate this area.
Substituting all these values into the total area formula
gives the total cross-sectional area of flow:
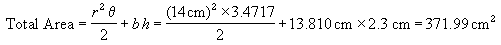
Converting this to square meters gives:
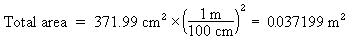
The last step is to find the volume flow (the volume of liquid
flowing through the pipe per unit time). This is given by the
cross-sectional area times the velocity:
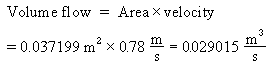
All that remains now is to convert this result to the desired
units, namely imperial gallons per minute:
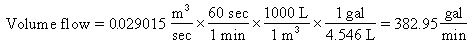
Because the information presented in this problem was accurate
to only 2 significant figures we must round our answer to 2
significant figures as well. Thus the flow rate of liquid waste
through the pipe is 380 gal/min.

Written by Louise Routledge, Thursday, December 12, 1996