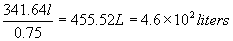A rectangular swimming pool, with a width of 6.1 m and the cross section as shown in the diagram below, is to be lined with epoxy paint. If a minimum dry coat thickness of 3.0 mm is required and the shrinkage upon drying is 25%, how many litres of paint are needed?
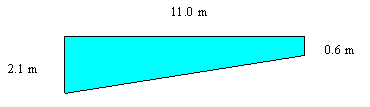
The pool has two trapezoidal sides as shown above. (Called Area 1).
The pool water on the top is flat, so each end wall will be rectangular.
Area 2 = "deep end" end wall which will be 2.1 x 6.1 m
Area 3 = "shallow end" which will be 0.6 x 6.1 m
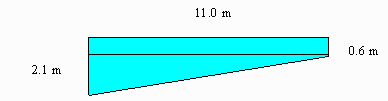
Area 4 = the bottom of the pool. If you look down at it from above the pool you will see it is a rectangle which is 6.1 m wide. We will get its length by creating a right angle triangle in the diagram above. The left side of the triangle will have length 2.1-0.6 = 1.5 m
The Interior Surface Area will consist of:
(Area 1 x 2) + (Area 2) + (Area 3) + (Area 4)
Area 1 = trapezoid:
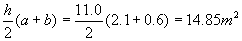
Area 2 = Rectangle:
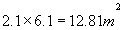
Area 3 = Rectangle:
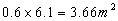
Find the length of the angled bottom wall of the pool by using the Pythagorean Theorem.
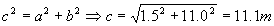
Area 4 = Rectangle:
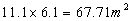
Total Area:
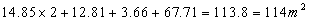
Imagine laying all the pieces out flat. You want these covered uniformly with a very thin layer of epoxy paint. In this case
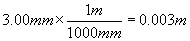
Thus the volume of paint required before shrinkage allotment.
Volume=Area x thickness:
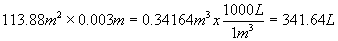
Since the paint shrinks by 25% of what you start with, then 75% of the total required = 341.64L
Total Paint Required:
Written by Louise Routledge, June 26, 1998