A phasor is a vector that represents a sinusoidal waveform. We will define a phasor by constructing one.
First we construct a vector of length A and at angle θ. The length, y, of the vertical component of the vector is given by trigonometry.
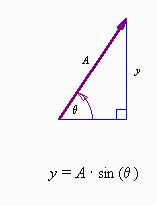
Now suppose that the angle θ increases with time so that the vector rotates counter-clockwise. To be specific let the angle be given by the formula shown here:
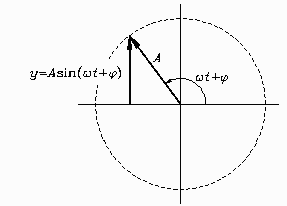
Notice that now the formula for the the vertical component is exactly the formula for a sinusoidal waveform.
This means that a sinusoidal waveform can be interpreted as the vertical component of a rotating vector!
What does this formula for the angle mean? It means that at time t = 0 the angle equals φ and that from then on the angle grows at the steady rate of ω radians per second.
The problem with rotating vectors is that since they are always moving, they are impossible to draw on a page! Thus we freeze them in at a certain time. This turns out to not be a limitation as long as all vectors in a problem are rotating at the same rate.
We define the phasor as follows:
Every sinusoidal waveform can be considered to be the vertical component of a rotating vector. A phasor is a snapshot of the rotating vector taken at the moment in time t = 0.
Thus, for example the waveform y= 5sin(100t+30°) is represented by the phasor y=5∠30°