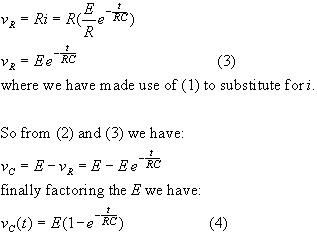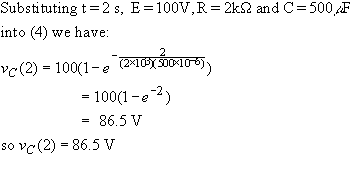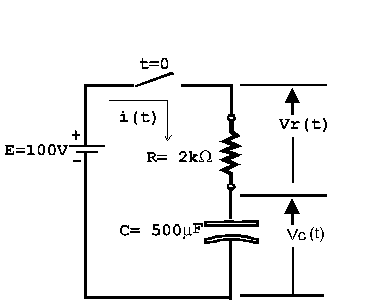
An RC circuit is one that contains a resistor and capacitor. Consider the RC circuit shown in the figure. Suppose that the switch is closed at time t = 0 s and that the capacitor has no initial stored charge on it. Once the switch closes, a current will begin flowing in the circuit. This current will deposit charge on the capacitor, leading to a voltage vC(t) across the capacitor.
The current i(t) is given by the formula:
(equation 1)
for 
where i is the current (in amperes),
E is the battery voltage (in volts),
R is the resistance (in Ohms,
Ω), C is the capacitance (in
Farads, F) and t is time (in seconds,
s).
Problem:
- Find a formula for the capacitor voltage vC(t).
- Given that E, R and C have the values shown in the diagram, find the capacitor voltage 2 seconds after the switch is closed.
- How long after the switch is closed will the capacitor voltage be equal to 70% of its final value?
(equation 2)
