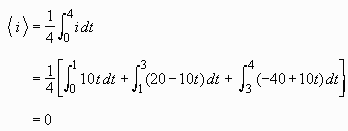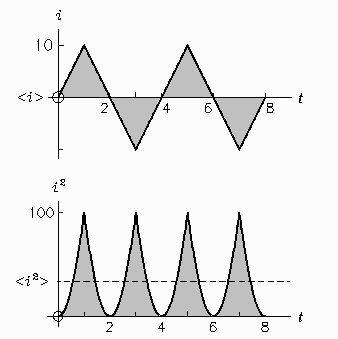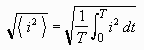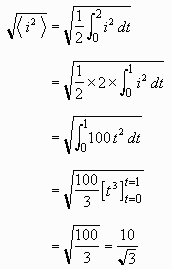Electronics:
Integrals and RMS Signals

Background

The average or mean of a set of numbers is found by adding up the numbers and dividing by the number of numbers. The mean value of a function is the generalization of this idea. The mean value of any function f(x) is defined as the mean height of the function. It can be found by calculating the area under the function and dividing by the width of the function. We will denote the mean value of a function f using angle brackets like this:

Then using calculus notation the above statement can be written as:

(We are assuming that the function runs from a to b, so integrating from a to b gives the area under the function and dividing by b - a divides by the width of the function.)

If the function is periodic (i.e. if the function repeats itself exactly after a certain amount of time, called the period, T) then we can replace the above formula by this formula:

In other words we only have to find the area for one cycle and divide by the width of one cycle.

The RMS value of a function is related to the idea of the standard deviation of a set of numbers. The RMS value of a function is defined as the square root of the mean value of the square of a function. In other words to get the RMS value of a function we follow these three steps:

  1. Square the function (i.e. draw a new function whose height everywhere is the square of the original function),
  2. calculate the Mean of this new function (This can be done using the above formula, namely, finding the area under the new function, and dividing by the width of the function),
  3. taking the square Root

We will denote the RMS value of a function f like this:

Then using calculus notation the above procedure can be written as:

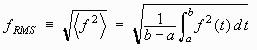
(Again we are assuming that the function runs from a to b, so integrating from a to b gives the area under the squared function and dividing by b - a gives the mean of the squared function.)

If the function is periodic with period T then we can replace the above formula by this formula:

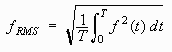
Problem

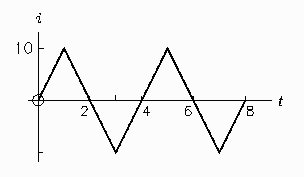
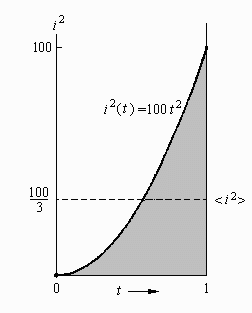
Find the mean value and RMS value of the triangular waveform shown to the right. It represents the current i flowing in a circuit as a function of the time, t.

Solution

The mean value of the current. Use the formula:

The period is T = 4. The integral from 0 to 4 must be broken into 3 separate integrals because the function has a different form in each section. The result is:

Thus the mean value of the current is zero. We could have gotten this result much more easily using symmetry rather than integration. The picture to the right shows the "area under the curve" shaded in grey. It is clear that the area from 0 to 2 is positive and the area from 2 to 4 is negative and that the two areas cancel out.

The RMS value of the current. Use the formula:

The lower picture shows the area under the i2 curve shaded in grey. Notice that the i2 curve has the period T = 2. In fact, notice that the area from 0 to 1 and the area from 1 to 2 are equal. Thus we will save work if we find the area from 0 to 1 and double our answer.

The picture to the right shows the region from t=0 to t=1 enlarged. Notice that in this region i = 10t, so i2 = 100t2

The result is:

Notice that the final answer is the peak value of the current (namely 10) divided by the square root of 3. In fact the RMS value for triangular waveforms with triangles of any shape turns out to always be the peak value divided by the square root of 3.

Return To Math ApplicationsPage

Written by Eric Hiob, June 12, 1998