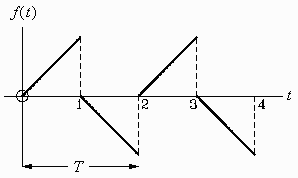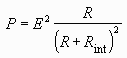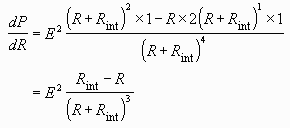Electronics: Using Derivatives with Circuits
A waveform is a function that repeats itself or cycles after a
specified period of time. This time, denoted T, is
called the period of the waveform.
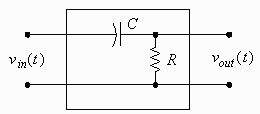
The diagram to the right shows an electronic circuit that takes
as input a voltage waveform and gives as output an approximation
of the derivative of that waveform. The approximation can be made
quite good by using small enough values of R and
C or restricting ourselves to slowly varying input
voltages.
To calculate the derivative of a waveform it is sufficient to
calculate the derivative of just the first cycle. This is because
the derivative of a waveform is another
waveform. The derivative of all the other cycles will
look the same as that of the first cycle. If f
(t) is the formula for the first cycle then f
′ (t), its derivative, is the formula for
the derivative of the first cycle. If required, the formula for
the derivative of any other cycle can be found by simply applying
a shift to the formula for the derivative of the first
cycle.
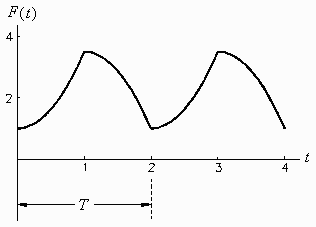
Problem
Calculate and sketch the derivative of the waveform shown to
the right, whose period is 2 seconds and whose first cycle is
defined as:
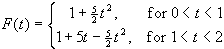
Solution
We begin by calculating the derivative,
F′(t), of the above formula:
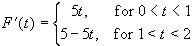
This is the formula for the first cycle of the derivative. Any
other cycle looks the same as the first one. A sketch of this
derivative is shown below.
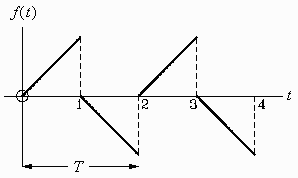
Problem
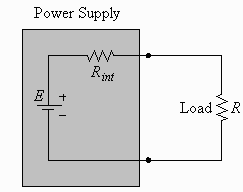
A power supply can be represented by an ideal voltage source
of E volts in series with an internal resistance
Rint. If a load is connected to the power supply, show that
the maximum power that can be supplied to the load is achieved
when the resistance R of the load is chosen to equal the
internal resistance Rint of the power supply.
Solution
We will express the power P dissipated in the
resistor R as a function of R and then find
where this function has its maximum. The power P
dissipated in a resistor R is given by the formula
P = I 2 R, where I
is the current flowing through the resistor. Expressing the
current I as a function of R (using
Ohm’s law) gives:
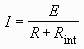
Now we can express the power P as a function of
R:
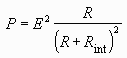
Notice that this function is zero when R is zero, is
positive for all positive values of R, and decreases
like 1/R when R is very large. Clearly
P must have a maximum. Now calculate the derivative
dP/dR:
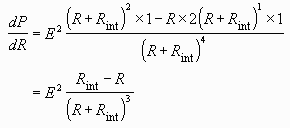
This derivative is equal to zero when R =
Rint. From the above discussion it is clear
that the derivative is zero here because this is the value of the
resistance R at which the power P is a
maximum (as opposed to say a minimum).

Written by Eric Hiob,
September 27, 1997