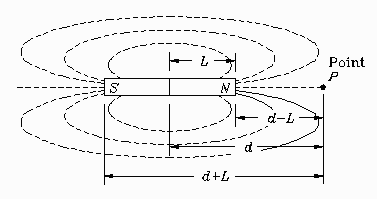
Consider the bar magnet shown. The
magnetic field strength H at a test point P
along the axis of the magnet is given by the formula:
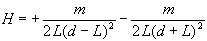
This formula was deduced from the following considerations.
Imagine a north pole (a monopole) located at test point P. The
north pole of the bar magnet repels the test monopole and the
south pole attracts it. The first term of the formula, with a +
sign, represents the field of the repulsive north pole, and the
second term, with a - sign, the attractive south pole. The
magnetic field due to either pole falls off as the inverse square
of the distance of the test point from the pole.
Problem:
Show that at large distances H falls off
as the inverse cube of the distance.
Solution
The phrase "at large distances" means
that the distance d becomes very large; much larger than
the distance L. If we let d become very large
in the original expression:
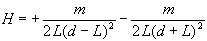
we simply get:
H = + 0 - 0
sinced is in the denominator. This is of no help. What is
required is to combine the two fractions into one. Start by
putting them over a common denominator, like this:
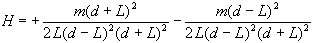
and adding:
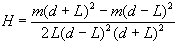
Now expand the numerator:
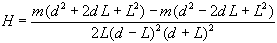
and simplify:
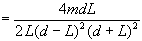
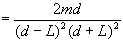
We can simplify further by noticing that the denominator can be
written as a difference of squares, squared:
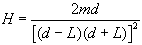
or finally:
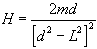
In this final expression we can see that if d is much
larger than L then we can neglect the
L2 inside the square brackets and get the
following:
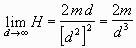
This proves that at large distances H falls off as the
inverse cube of the distance.
Solution
The formula for resistors in series gives:
R1 + R2 = 10.
The formula for resistors in parallel gives:
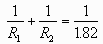
or making a single fraction:
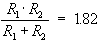
These equations form a simultaneous system of equations because
the solutions R1 and R2
must satisfy both equations simultaneously. One method to solve
this system is to solve the first equation for say R1:
R1 = 10 -
R2
and to then substitute this expression for R1
into the second equation wherever R1
occurs:
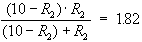
This is called the method of substitution. We can now solve this
equation for R2. Clearing the denominator and
getting everything to the left-hand-side gives:
(10 - R2) · R2 - 18.2 = 0
or
R22 - 10 R2 + 18.2 = 0
Solving this by the quadratic formula, we get:
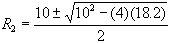
The two solutions are R2 = 7.61 and
R2 = 2.39. To get a value for R1 we can go back to the series equation:
R1 + R2 = 10.
This equation tells us that if we let R2=7.61
ohms then R1=2.39 ohms. And if we let
R2=2.39 ohms then R1=7.61
ohms.
