Chemical Science - Logs & Exponents: Newton’s Law of Cooling

Keanu Lapaloosa, a conscientious BCIT lab assistant has just heated up a solution of sodium hydroxide, (NaOH), to 225° F as part of an experiment. He then puts the solution inside a fumehood for cooling and finds that it cools from 225° F down to 185° F in 5.0 minutes. If the temperature inside the fume hood is a constant 60° F, find, using Newton’s Law of Cooling:

  1. the time it takes the solution to cool from 225° F to 120° F
  2. the temperature of the solution after 30 minutes in the fume hood.

Solution:

Newton’s Law of Cooling states:

Where T is the temperature of a cooling object at time t , T 0 is the temperature of the object at time t = 0, T s is the temperature of the surrounding medium, and k is the decay constant.

For this problem,

(1)

The first thing we need to do is find k .

Substituting T = 185° F, when t = 5.0 minutes, into (1), we get:

And, simplifying, we get:

Taking natural logs of either side, we get: ln(125) - ln(165) = -5.0 k

And

(2)

  1. To find how long it will take for T to reach 120° F, we substitute into (2) and solve for t

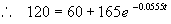    , and simplifying, we get:

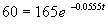
    Taking natural logs of either side, we get: ln(60) - ln(165) = -0.0555 t

    And

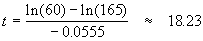
    ∴ it will take about 18.0 minutes for the solution to cool down to 120° F

  2. To find the temperature of the solution after t = 30 minutes, we substitute again into (2)

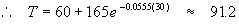
    So we find that after 30 minutes, the temperature of the solution will be about 91° F.

Return To Math ApplicationsPage
Written by Arch McFarlane, June 2003